on my way
C++ 알고리즘:: 시간 복잡도 Big O 본문
시간복잡도란 알고리즘 스피드의 표현법이다.
같은 알고리즘이더라도, 컴퓨터마다 속도가 다르다.
왜냐하면 컴퓨터라는 하드웨어가 결정하기 때문이다.
따라서 알고리즘은 완료까지 걸리는 절차의 수로 표현이 된다.
Linear Search(선형 검색)
선형 검색이란 한개씩, 한개씩 검색을 하는 것이다.
따라서 데이터가 10개라면, 10개의 스텝이 필요한 것이다.
인풋 사이즈가 N이라면, 선형 검색 알고리즘은 N번이 필요하다.
선형 검색의 시간 복잡도는 O(N)이다.
따라서 선형검색은 y=x 그래프 모양이다.
빠르고, 이해가 쉬운 형태이다.
이런 표현법을 시간복잡도 표기법을 Big O라고 표현한다.
이런 방법으로 나의 코드의 성능을 확인할 수 있다.
만약 배열에서 다음과 같이 요소 하나만을 읽는 코드라면
print(arr[0])Big O에서 읽는 방법은 O(1)이다.
물론 배열의 요소 두개를 읽는 코드도 O(2)가 아닌 O(1)이다.
왜냐하면 Big O는 함수의 디테일에는 관심이 없기 때문이다.
그저 input 사이즈에 따라서 달라진다.
즉, 미리 정해진 숫자에 따라 작동을 하게 된다. 상수(constant)에는 상관하지 않는다.
만약 200 스텝의 함수라면 인풋 사이즈에 상관하지 않고 그저 O(1)인 것이다.
O(1)은 y=1 그래프로 나타낼 수 있다.
늘 선호되는 알고리즘이지만 이런 알고리즘으로 만들기에는 어렵다.
for n in arr:
print(n)같은 코드가 있을 때,
배열이 10사이즈라면 출력할 때 10번 반복된다.
배열이 커지면 이에 따라 작동하므로 O(n)인 것이다.
또한 이 과정을 두번 반복하더라도 O(2n)이 아닌, 상수를 버린 O(n)이다.
Quadratic Time(2차 시간)
중첩 반복이 있을 때 발생하게 된다.
루프안에서 루프가 실행된다면, 20개의 데이터는 400개의 스텝이 된다. O(n^2)
즉, 이것보다는 선형 시간복잡도가 선호된다.
로그 시간
이진 검색 알고리즘에서 설명된다. (Binary Linear Search)
이진 검색에서는 절반으로 나누어서 스텝이 진행이 되기 때문에 O(log n)이 된다.
로그는 지수와 반대 개념이다.
n = log2(32)일 때
로그 n은 몇 번을 나누어야 값이 나오는 것인지 생각을 해보면 이해하기 쉬울 것이다.
이진 검색에서는 input을 일단 반으로 나누고 시작한다.
그렇기 때문에 input이 커져도 스텝은 +1만 증가한다.
(한번만 더 나누면 되기 때문이다.)
따라서 이진검색의 시간 복잡도는 O(log N)이다.
선형시간 보다 빠르고, 상수 시간보다는 느리다.
또한 이진 검색은 정렬되지 않은 배열에서 사용할 수 없다.
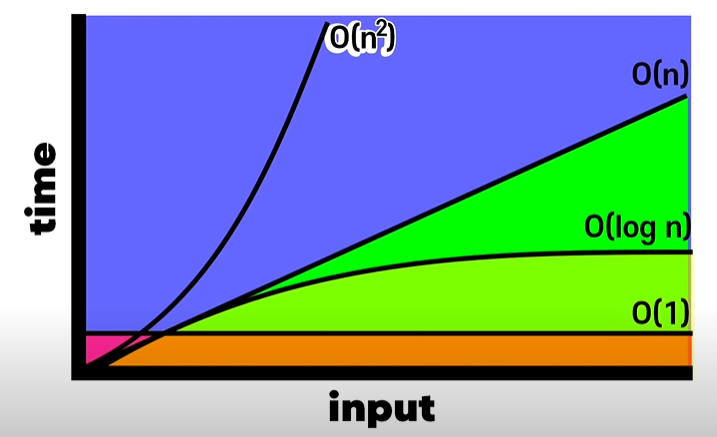
출처 : https://www.youtube.com/watch?v=BEVnxbxBqi8&list=PL7jH19IHhOLMdHvl3KBfFI70r9P0lkJwL&index=5
'algorithm > CodingTest' 카테고리의 다른 글
| C++ 알고리즘:: 다이나믹 프로그래밍 (0) | 2021.10.30 |
|---|---|
| C++ 알고리즘:: 완전 탐색(Brute-Force) & 백트레킹(Backtracking) (2) | 2021.10.24 |
| C++ 알고리즘:: 스택(Stack), 큐(Queue), 덱(Deque) (1) | 2021.10.11 |
| C++ 알고리즘:: 정렬 알고리즘 정리 (버블 정렬, 선택 정렬, 삽입 정렬, 퀵 정렬, 병합 정렬) (0) | 2021.10.03 |
| C++ 알고리즘:: Fast I/O, C++ STL (0) | 2021.09.26 |


