on my way
Python 코딩테스트 10: 최소 신장 트리 (Minimum Spanning Tree, MST) 본문
Python 코딩테스트 10: 최소 신장 트리 (Minimum Spanning Tree, MST)
wingbeat 2024. 8. 29. 20:39최소 신장 트리(MST)는 그래프 이론에서 사용되는 개념으로, 최소한의 비용으로 그래프의 모든 노드를 연결하는 트리를 의미합니다.
이 글에서는 MST의 기본 개념, 유명한 알고리즘, Python 구현 방법, 그리고 코딩 테스트에서 어떻게 활용될 수 있는지에 대해 알아보겠습니다.
1. 최소 신장 트리(MST)란?
그래프에서 신장 트리(Spanning Tree)는 그래프의 모든 노드를 포함하면서 사이클이 없는 트리 구조입니다.
이 중에서 최소 신장 트리(Minimum Spanning Tree)는 모든 노드를 연결하는 트리들 중에서 간선의 가중치 합이 가장 작은 트리를 의미합니다.
- 가중치 그래프: 노드 간의 연결 비용(간선의 가중치)이 있는 그래프.
- MST의 조건:
- 사이클이 없다.
- 그래프의 모든 노드를 포함한다.
- 간선의 가중치 합이 최소이다.
MST의 활용
MST는 네트워크 설계(예: 전력망, 통신망), 도로 연결, 클러스터링 등 다양한 분야에서 사용됩니다.
코딩 테스트에서도 MST는 주로 크루스칼(Kruskal) 또는 프림(Prim) 알고리즘을 이용해 문제를 해결합니다.
2. MST를 찾는 알고리즘
2.1. 크루스칼 알고리즘 (Kruskal’s Algorithm)
크루스칼 알고리즘은 모든 간선을 가중치 기준으로 정렬한 뒤, 가중치가 가장 작은 간선부터 선택하여 트리를 확장해가는 방법입니다.
이때, 사이클이 발생하지 않도록 유니온 파인드(Union-Find) 자료구조를 사용합니다.
- 시간 복잡도: (O(E \log E)), (E)는 간선의 수
이 그래프에서 나올 수 있는 신장 트리는 다음과 같이 여러 가지가 있을 수 있습니다.

그래프 중 위의 그래프와 같이 간선의 '비용'(혹은 가중치)이 존재하는 그래프도 있는데, 이때 '신장 트리' 중 그 비용의 합이 최소가 되는 신장 트리를 최소 신장 트리라 합니다.
상기 그래프의 경우 다음 신장 트리가 최소 신장 트리가 됩니다.

- 알고리즘 순서:
- 간선들을 가중치 기준으로 오름차순 정렬합니다.
- 가장 작은 가중치의 간선을 선택하고, 해당 간선을 MST에 추가합니다.
- 이때, 선택된 간선이 사이클을 형성하지 않도록 유니온 파인드를 이용해 검사합니다.
- 트리에 포함된 간선의 수가 (V-1) (노드의 수 - 1)이 될 때까지 반복합니다.
class UnionFind:
def __init__(self, size):
self.parent = list(range(size))
def find(self, u):
if self.parent[u] != u:
self.parent[u] = self.find(self.parent[u])
return self.parent[u]
def union(self, u, v):
root_u = self.find(u)
root_v = self.find(v)
if root_u != root_v:
self.parent[root_v] = root_u
def kruskal(edges, num_nodes):
uf = UnionFind(num_nodes)
mst_weight = 0
edges.sort(key=lambda x: x[2]) # 간선 가중치로 정렬
mst_edges = []
for u, v, weight in edges:
if uf.find(u) != uf.find(v):
uf.union(u, v)
mst_weight += weight
mst_edges.append((u, v, weight))
return mst_weight, mst_edges
# 예시 그래프: 간선 리스트 (u, v, weight)
edges = [
(0, 1, 10), (0, 2, 6), (0, 3, 5),
(1, 3, 15), (2, 3, 4)
]
num_nodes = 4 # 노드의 수
print(kruskal(edges, num_nodes))2.2. 프림 알고리즘 (Prim’s Algorithm)
프림 알고리즘은 시작 노드에서부터 트리를 확장해 나가는 방식입니다. 항상 현재 트리에 연결 가능한 간선 중에서 가중치가 가장 작은 간선을 선택합니다. 이 과정에서 우선순위 큐를 사용하면 효율적으로 트리를 확장할 수 있습니다.
- 시간 복잡도: (O(E \log V)), (V)는 노드의 수, (E)는 간선의 수
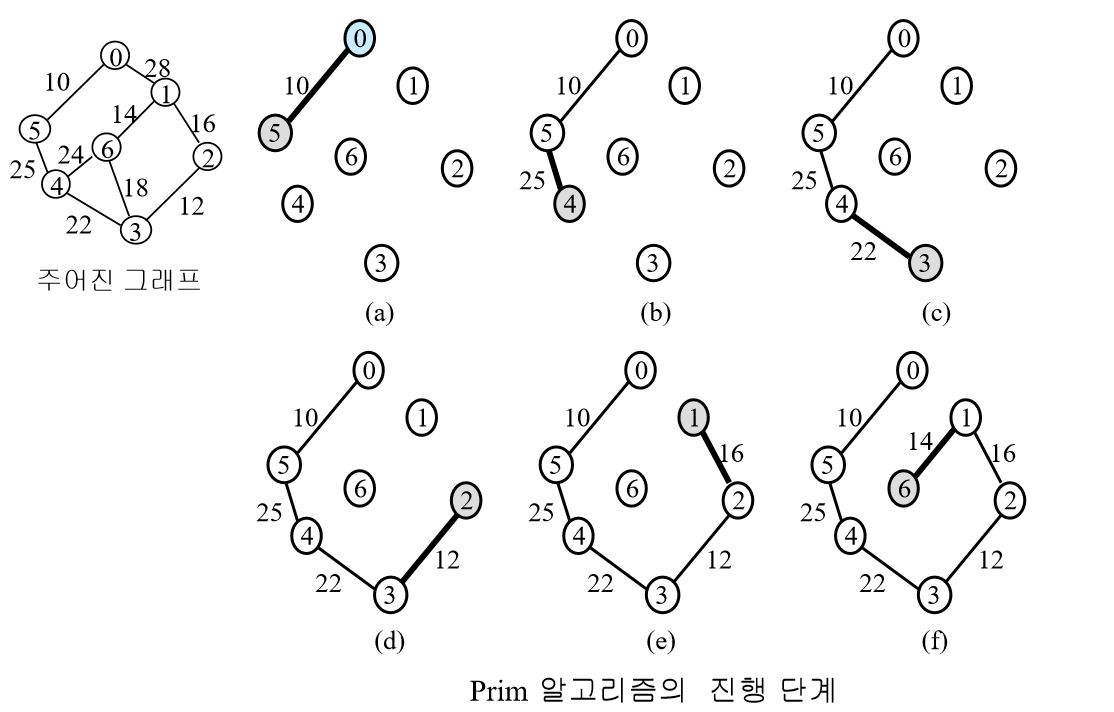
- 알고리즘 순서:
- 임의의 노드를 시작으로 선택합니다.
- 트리에 포함된 노드와 연결된 간선 중에서 가중치가 가장 작은 간선을 선택합니다.
- 선택된 간선의 상대 노드를 트리에 추가합니다.
- 모든 노드가 트리에 포함될 때까지 반복합니다.
import heapq
def prim(graph, start):
mst_weight = 0
visited = [False] * len(graph)
priority_queue = [(0, start)] # (가중치, 노드)
while priority_queue:
weight, u = heapq.heappop(priority_queue)
if not visited[u]:
visited[u] = True
mst_weight += weight
for v, w in graph[u]:
if not visited[v]:
heapq.heappush(priority_queue, (w, v))
return mst_weight
# 예시 그래프: 인접 리스트
graph = {
0: [(1, 10), (2, 6), (3, 5)],
1: [(0, 10), (3, 15)],
2: [(0, 6), (3, 4)],
3: [(0, 5), (1, 15), (2, 4)]
}
start_node = 0
print(prim(graph, start_node))3. MST가 활용되는 코딩 테스트 문제
3.1. 네트워크 연결 문제
문제: 여러 개의 컴퓨터가 네트워크로 연결되어 있습니다. 이때 모든 컴퓨터를 연결하는데 드는 최소 비용을 계산하는 문제입니다.
- 풀이 전략: 그래프의 모든 노드를 최소 비용으로 연결해야 하므로, MST를 찾는 문제가 됩니다. 크루스칼 또는 프림 알고리즘을 사용하여 풀이할 수 있습니다.
3.2. 도로 건설 문제
문제: 여러 도시를 도로로 연결할 때, 모든 도시를 연결하는데 필요한 최소 비용을 계산하는 문제입니다.
- 풀이 전략: 마찬가지로, 모든 도시를 연결하는 최소 비용을 구해야 하므로 MST를 이용해 풀 수 있습니다.
4. MST 문제 해결 시 주의할 점
- 사이클 방지: MST는 트리 구조이므로 사이클이 있으면 안 됩니다. 이를 위해 크루스칼 알고리즘에서는 유니온 파인드 자료구조를 사용해 사이클을 방지합니다.
- 우선순위 큐 활용: 프림 알고리즘을 구현할 때 우선순위 큐를 활용하면 간선 선택을 효율적으로 할 수 있습니다.
- 그래프 표현 방식: 인접 리스트와 간선 리스트 중 상황에 맞는 표현 방식을 선택해야 합니다. 크루스칼은 간선 리스트, 프림은 인접 리스트가 일반적입니다.
최소 신장 트리는 코딩 테스트에서 빈번히 출제되는 주제입니다.
크루스칼과 프림 알고리즘을 통해 MST를 효율적으로 찾는 방법을 숙지하고, 다양한 문제에 적용할 수 있어야 합니다.
'algorithm > CodingTest' 카테고리의 다른 글
| Python 코딩테스트 09: 정렬 (0) | 2024.08.29 |
|---|---|
| Python 코딩테스트 08: 다이나믹 프로그래밍 DP (2) | 2024.08.07 |
| Python 코딩테스트 08: 다익스트라 알고리즘 (1) | 2024.07.29 |
| Python 코딩테스트 07: 백트래킹 (0) | 2024.07.29 |
| Python 코딩테스트 06: 투포인터와 슬라이딩 윈도우 (0) | 2024.07.29 |


