on my way
3D 게임 프로그래밍 기초 수학 2 :: 벡터의 뺄셈, 벡터와 스칼라의 곱셈 본문
벡터의 뺄셈
뺄셈을 할 때는 수식에서 그대로 -로 표현하여 덧셈하면 된다.
벡터에 -를 붙인다는 것은, 크기는 그대로 두변서 방향만 반대로 바꾸는 것이다.
즉 B-A는 B+(-A)이다.
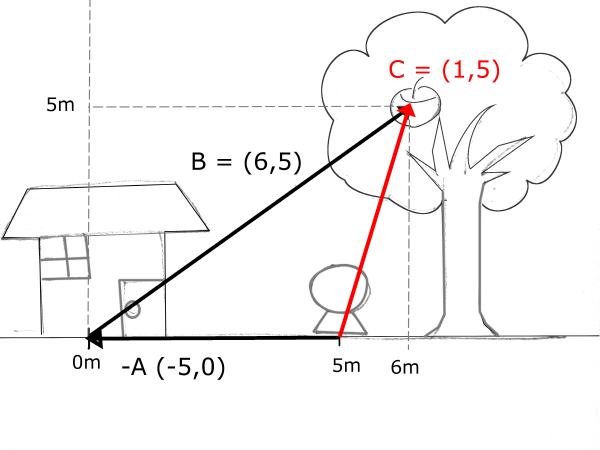

벡터의 덧셈이란 시작점의 꼬리에서 끝점의 머리까지 잇는 것이다.
즉, 뺄셈도 방향만 바꾸어 그대로 적용하면 위와같은 C 벡터를 얻을 수 있다.
또한 오른쪽 그림처럼 두 빨간 벡터는 크기와 방향이 같기 때문에 완전히 동일한 벡터이다.
따라서 벡터의 뺄셈은 위처럼
특정 위치에서 다른 위치를 향하는 벡터를 구할 때 사용하면
쉽게 해당 벡터를 구할 수 있다.
게임 프로그래밍에서는 캐릭터를 특정 장소로 움직이도록 만들 때 사용한다.
예를 들어 플레이어를 추적하는 몬스터를 구현할 때
몬스터가 플레이어의 현재 위치를 향해 매 프레임 이동하는 로직으로 구상할 수 있다.
그렇다면 몬스터의 x, y좌표에 어떤 계산을 해야할까?
이 때, 몬스터의 이동 방향을 구하는데 벡터의 뺄셈을 활용할 수 있다.
플레이어를 향하는 방향 = 플레이어의 위치 - 몬스터의 위치
몬스터의 위치와 플레이어의 위치을 벡터로 간주한다면, 벡터의 뺄셈을 그대로 적용할 수 있다.
계산된 결과는 몬스터에서 플레이어를 잇는 벡터가 된다.
이 벡터를 따라서 몬스터를 움직이게 하면 된다.
TIP🌟
실제 코드를 구현할 때는 이 벡터를 단위 벡터로 만든 뒤,
몬스터의 이동 속력을 곱하여, 최종적으로 속도 벡터를 얻는 과정이 필요하다.
방향 벡터 = 플레이어의 현재 위치 – 몬스터의 현재 위치
방향 벡터를 단위 벡터로 만들고 이동 속력을 곱해 속도 벡터를 계산
몬스터의 새로운 위치 = 몬스터의 현재 위치 + 시간 * 속도 벡터
벡터와 스칼라의 곱셈
스칼라란 일반적인 수이다.
A=[5,0]인 벡터가 있을 때, 스칼라 d를 곱해준다면
A*d=[5,0]*2=[10,0]이다.
게임 프로그래밍에서는 방향 벡터에 속력을 곱해서
속도 벡터를 만드는 데 사용할 수 있다.
벡터의 뺄셈 정리
1. 뒤에 있는 벡터의 방향을 반대로 바꾼다.
B-A 라면 A벡터의 방향을 반대로 바꾼다.
방향을 바꾸는 것은 길이는 그대로 두고 화살표가 가리키는 곳만 반대로 만들어 주는 것을 의미한다.
2. 두 벡터를 덧셈 규칙에 맞게 꼬리에서 머리로 이어준다.
3. 벡터의 뺄셈은 한 위치에서 다른 위치로 향하는 벡터를 만들 때 사용할 수 있다.
출처: http://lab.gamecodi.com/board/zboard.php?id=GAMECODILAB_Lecture_series&page=1&sn1=&divpage=1&sn=off&ss=on&sc=on&select_arrange=headnum&desc=asc&no=123
3D 기초 수학 강좌 - 3. 벡터의 밸셈, 벡터와 스칼라의 곱셈
lab.gamecodi.com
'Computer Science > IT MATH' 카테고리의 다른 글
| 3D 게임 프로그래밍 기초 수학 6 :: 삼각함수 원, 라디안, 파이 (0) | 2021.09.26 |
|---|---|
| 3D 게임 프로그래밍 기초 수학 5 :: 삼각함수 sin, cos, tan (0) | 2021.09.26 |
| 3D 게임 프로그래밍 기초 수학 4 :: 벡터의 외적 (0) | 2021.09.26 |
| 3D 게임 프로그래밍 기초 수학 3 :: 벡터의 내적 (0) | 2021.09.26 |




