on my way
3D 게임 프로그래밍 기초 수학 3 :: 벡터의 내적 본문
내적 (스칼라 곱 or 점곱, dot product, inner product)

물체가 빛을 받으면 밝은 부분과, 어두운 부분이 생긴다.
이런 명암을 컴퓨터 그래픽으로 모델링할 때 벡터의 내적 연산이 사용된다.

왼쪽은 렌더링 된 결과물, 오른쪽은 카메라와 물체의 관계를 옆에서 본 모습이다.
파란색 벡터 A,B,C,D는 각 벡터의 법선 벡터이다.
법선벡터 (노말벡터)
어느 표면에 붙어있던 해당 표면에 수직인 벡터이다.

검은색 선은 각 폴리곤으로부터 카메라쪽으로 향하는 벡터를 나타낸 것이다.
그림으로 봤을 때, 두 벡터 사이의 각도가 90도 이하이면
해당 폴리곤은 해당 카메라를 바라보고 있다고 판단할 수 있다. (A, B)
반대로 90도보다 크면 카메라를 등지고 있다고 판단할 수 있다. (C, D)
카메라를 등지고 있는 폴리곤은 어차피 보이지 않을 것이므로, 계산에서 제외하면 랜더링 성능이 올라갈 것이다.
그렇다면 내적은 도대체 어떻게 계산되는 것일까?
내적의 계산 과정
벡터의 내적을 계산하기 위해서는 먼저 차원이 같은 두 벡터가 필요하다.
벡터의 각 성분들끼리 곱셈을 한 뒤, 결과를 더해주면 내적이 계산된다.
A = [2, 2]
B = [-1, 0]
A∙B = [2 * -1] + [2 * 0] = -2 + 0 = -2
C = [-2,-2]
B = [-1, 0]
C∙B = [-2 * –1] + [-2 * 0] = 2 + 0 = 2
여기 알 수 있는 사실!
두 벡터를 내적하면 벡터가 나오는 것이 아닌, 단순한 숫자값이 나온다.
또한 이 결과값의 부호를 통해서 폴리곤의 면이 카메라를 향하고 있는지, 등지고 있는 지를 알 수 있다.
내적의 결과가 양수(+)라면, 두 벡터 사이의 각이 90도 보다 같거나 작다는 뜻이고
결과가 음수(-)라면, 두 벡터 사이의 각이 90도 보다 크다는 뜻이다.

즉, 그림의 벡터 A와 B를 각각 카메라를 향하는 벡터와 내적을 하면
그 결과값은 양수로 나오게 되며, 두 벡터 사이의 각은 90도 보다 작다.
반대로 벡터 C와 D를 각각 카메라를 향하는 벡터와 내적을 하면
그 결과값은 음수로 나오게 되며, 두 벡터 사이의 각은 90도 보다 크다.
여기서 중요한 것은 각도가 몇 도 인지까지 계산할 필요 없이,
내적의 결과값의 부호만으로 각도의 범위를 알아낼 수 있다.
두 벡터 사이의 각도를 구하려면 삼각학수인 arccos(acos, 아크코사인) 함수를 사용해야하는데
삼각함수를 많이 사용하면 프로그램의 성능이 하락될 수 있기 때문에
몇 번의 곱셈과 덧셈으로 끝나는 내적을 사용하는 것이 훨씬 이득이다.
반사 벡터 구하기
내적을 이용하여 반사벡터를 쉽게 구할 수 있다.
벽에 부딪힌 공이 어느 방향으로 튕겨나가는 지 상상한다면
반사 벡터의 모습을 머릿 속에서 그려볼 수 있을 것이다.
벡터 p가 공의 속도벡터라고 하자. 그렇다면 반사벡터를 구하는 공식은
reflect = p + 2n(-p*n)
n은 벽의 법선 벡터이다.
이 공식을 프로그래밍 언어로 구현한다면 다음과 같다.
Vector3 reflect = velocity + 2 * normal * Vector3.Dot(-velocity, normal);


공은 벽을 향해 대각선 방향인 p의 속도로 움직이고 있다.
여기서 p는 공의 속도 벡터이다.
-p는 반사 벡터를 구하기 위한 첫번째 과정으로, p의 방향을 바꿔준다.
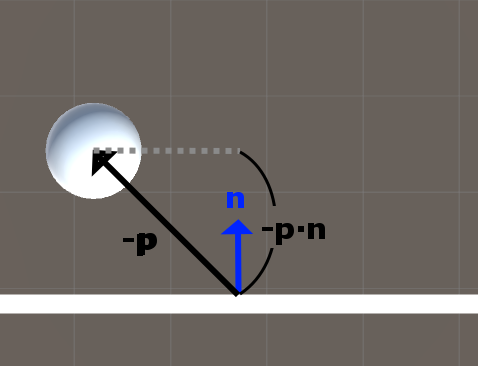

-p * n : -p와 벽의 법선 벡터인 n을 내적하면, 내적의 결과로 스칼라값 -p*n 하나가 나온다.
2n(-p*n)) : 내적의 결과값과 법선벡터 n을 2배하여 곱한다.
결과적으로 법선벡터 n을 길게 늘려준 벡터가 생긴다.
(-p*n)은 스칼라 값이고, 여기에 n을 곱하면 벡터 n의 길이는 벡터 -p의 높이 성분과 같은 길이를 같게 된다.
여기에 2를 곱하면, 길이가 2배로 늘어난 벡터가 된다.
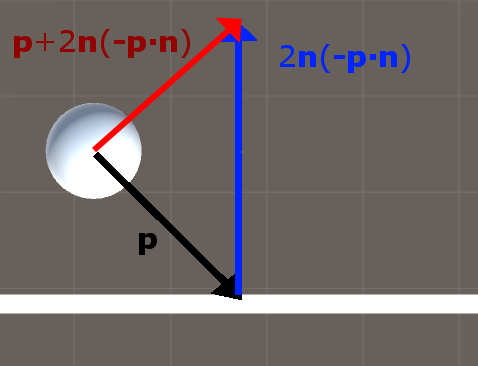

따라서 p+2n(-p*n) : 위의 결과 값에 p를 더해서 반사 벡터를 구한다.
크기와 방향 같으니 어디에 있던지 결국에 똑같은 벡터이다.
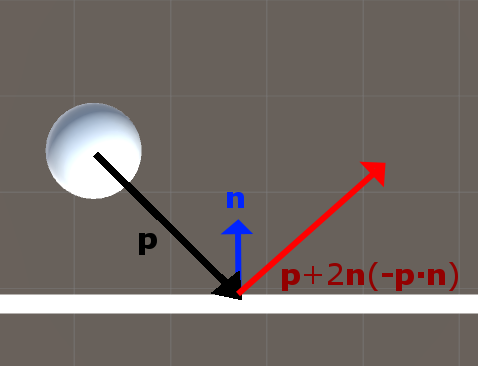
최종적으로 p의 반사 벡터가 구해졌다.
투영
반사 벡터를 구하며 내적의 쓰임새를 알아봤다.
이해해야 할 부분은, 벡터의 내적을 통해 한 벡터가 다른 벡터에 투영된 길이를 알 수 있다는 것이다.
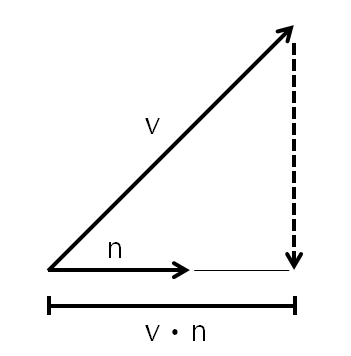
투영은 어떤 벡터 v 를 단위 벡터 n 에 내적하여, v 의 n 방향으로의 길이를 구하는 것을 말한다.
투영이란 그림자라고 이해하면 된다.

내적값은 스칼라이므로,
투영된 방향으로 벡터를 구하려면 내적값(v*n)에 방향벡터 n을 곱해주어야 한다.
반사 벡터를 구할 때 벡터 -p를 벽의 법선 벡터인 n과 내적하여 계산했는데,
이 내적의 결과로 나온 값은 벡터 -p를 법선 벡터 n에 투영한 길이가 된다.
단, 법선벡터 n은 반드시 단위 벡터 상태로 되어 있어야 한다. (단위벡터 : 길이가 1인 벡터)

벡터 n을 위로 쭉 그린다고 생각하면 가상의 선이 그려질 것이다.
이 선을 따라서 벡터 -p를 직선으로 그었을 때 만나는 점, 그 점의 길이가 바로 내적의 결과값이다
이 그림에서는 점선으로 표시한 부분과, 벡터 n의 연장선이 만나는 지점이 된다.
출처 : https://ifyouwanna.tistory.com/entry/%EB%B0%98%EC%82%AC%EB%B2%A1%ED%84%B0http://lab.gamecodi.com/board/zboard.php?id=GAMECODILAB_Lecture_series&page=1&sn1=&divpage=1&sn=off&ss=on&sc=on&select_arrange=headnum&desc=asc&no=126
반사벡터
1. 투영벡터 - 반사벡터를 구하기 위해선 먼저 벡터의 투영에 대해서 알아야 한다. - 투영은 어떤 벡터 v 를 단위 벡터 n 에 내적하여, v 의 n 방향으로의 길이를 구하는 것을 말한다. - 내적값은 스
ifyouwanna.tistory.com
3D 기초 수학 강좌 - 5. 벡터의 외적
3D 게임 프로그래밍을 위한 ...
lab.gamecodi.com
'Computer Science > IT MATH' 카테고리의 다른 글
| 3D 게임 프로그래밍 기초 수학 6 :: 삼각함수 원, 라디안, 파이 (0) | 2021.09.26 |
|---|---|
| 3D 게임 프로그래밍 기초 수학 5 :: 삼각함수 sin, cos, tan (0) | 2021.09.26 |
| 3D 게임 프로그래밍 기초 수학 4 :: 벡터의 외적 (0) | 2021.09.26 |
| 3D 게임 프로그래밍 기초 수학 2 :: 벡터의 뺄셈, 벡터와 스칼라의 곱셈 (0) | 2021.09.25 |





